Matematika Kelas 7: Bilangan Bulat dan Bilangan Pecahan

- Bilangan Bulat

Bilangan bulat termasuk bilangan rasional yang merupakan bagian dari bilangan real, dan juga bilangan bulat terdiri dari:

Bilangan bulat negatif = {...,–5,–4,–3,–2,–1}
Bilangan nol = {0}
Bilangan asli atau bilangan bulat positif = {1,2,3,4,5,...}. Bilangan asli terbagi menjadi:

Bilangan ganjil = {1,3,5,7,...}
Bilangan genap = {2,4,6,8,...}

Bilangan bulat dapat dibagi menggunakan Garis Bilangan

1. Mengurutkan Bilangan Bulat

Mengurutkan beberapa bilangan bulat, yaitu menuliskan bilangan bulat tersebut secara urut dari yang nilainya terbesar atau terkecil. Pada garis bilangan, semakin ke kanan letak suatu bilangan, nilainya semakin besar. Sebaliknya, semakin ke kiri, nilainya semakin kecil.

2. Membandingkan Bilangan Bulat

Lambang-lambang untuk membandingkan dua bilangan bulat sebagai berikut:

2 lebih dari 1, ditulis 2 > 1
1 kurang dari 2, ditulis 1 < 2
2 lebih dari atau sama dengan 1, ditulis 2 ≥ 1
1 kurang dari atau sama dengan 2, ditulis 1 ≤ 2

Bilangan positif selalu lebih besar dari bilangan negatif

3. Lawan (Invers) Suatu Bilangan Bulat

Lawan bilangan 1 adalah –1. Sebaliknya, lawan –1 adalah 1.

Contoh:

lawan 5 adalah –5
Invers dari –3 adalah 3

Operasi Hitung Bilangan Bulat

Operasi hitung penjumlahan pada bilangan bulat dapat menggunakan alat bantu berupa :

Mistar hitung
Mistar hitung adalah alat bantu untuk menghitung penjumlahan pada bilangan bulat yang dapat dibuat sendiri dari kertas karton. Mistar hitung yang akan digunakan terdiri dari dua buah mistar dengan skala yang sama dan terdiri dari bilangan bulat, yaitu bilangan bulat negatif, nol dan bilangan bulat positif.

Garis Bilangan
Sebuah garis bilangan dapat digunakan untuk membantu penjumlahan pada bilangan bulat.

Jika suatu bilangan dijumlah dengan bilangan bulat positif, maka arah panah ke kanan dan jika dijumlah dengan bilangan bulat negatif, maka arah panah ke kiri.

Contoh :
a. 3 + 4 = 7 b. 3 + (-8) = -5

Penjumlahan bilangan bulat

Pada himpunan bilangan Bulat terdapat pasangan-pasangan bilangan bulat positif dan bulat negatif.

5 berpasangan dengan –5, maka 5 lawan dari –5
– 3 berpasangan dengan 3, maka –3 lawan dari 3

Sehingga :

Lawan (invers jumlah) dari a adalah –a
Lawan (invers jumlah) dari –a adalah a

Pengurangan suatu bilangan merupakan penjumlahan bilangan itu dengan lawan pengurangnya.

Contoh :

Dengan menggunakan invers jumlah, tentukan hasil pengurangan bilangan-bilangan berikut :
- 4 – 6 = ………
- 8 – (- 2) = ………
- – 5 – (- 5) = ………..
- – 3 – 5 = …………….
Jawab :
- 4 – 6 = 4 + (-6) = -2
- 8 – (-2) = 8 + 2 = 10
- -5 – (-5) = -5 + 5 =0
- –3 – 5 = -3 + (-5) = – 8
Tanpa menggunakan invers jumlah, tentukan hasil pengurangan bilangan-bilangan berikut :

–6 – (-5) = ………….
–9 – 4 = ………….
12 – (-20) = ……….
–34 – (–22) = ……

Jawab :

–6 – (-5) = -1

–9 – 4 = -13

12 – (–20) = 32

–34 – (–22) = -10

Perkalian bilangan bulat

Arti perkalian

2 x 3 = 3 + 3
= 6

4 x 5 = 5 + 5 + 5 + 5

= 20

Perkalian bilangan bulat positif dan bilangan bulat negatif

3 x (-6) = -6 + (-6) + (-6)

= -18

4 x (-12) = -12 + (-12) + (-12) + (-12)

= -48

Perkalian bilangan bulat negatif dan bilangan bulat positif

Perkalian bilangan bulat negatif dan bilangan bulat negatif

Contoh :
Tentukan hasil perkalian bilangan-bilangan :

12 x (- 3) = …………..
16 x (- 4) = …………..
– 5 x 13 = …………..
16 x (- 7) = …………..

Jawab :

Tentukan hasil perkalian bilangan-bilangan :

12 x (- 3) = – ( 12 x 3 ) = – 36
16 x (- 4) = – ( 16 x 4 ) = – 64
– 5 x 13 = – ( 5 x 13 ) = – 65
– 16 x (- 7) = 16 x 7 = 112

Pembagian pada bilangan bulat

Arti pembagian.

Operasi pembagian merupakan kebalikan dari operasi perkalian

18 : 3 = 6 6 x 3 = 18

36 : 4 = 9 9 x 4 = 36

Pembagian bilangan bulat negatif dan bilangan bulat positif

Pembagian bilangan bulat positif dan bilangan bulat negatif

Pembagian bilangan bulat negatif dan bilangan bulat negatif

Contoh :
Hitunglah :

12 : (- 3) = …
16 : (- 4) = …
– 45 : 3 = …
– 63 : (- 7) = …

Jawab :

12 : (- 3) = – ( 12 : 3 ) = – 4
16 : (- 4) = – ( 16 : 4 ) = – 4
– 45 : 3 = – ( 45 : 3 ) = – 15
– 63 : (- 7) = 63 : 7 = 9

Contoh :
Jika p = – 48 dan q = 2, tentukanlah nilai dari :

2p : 3q
(p : 3) : q

Jawab :

2p : q = (2 x (- 28)) : 2

= – 56 : 2

= – 28

(p : 3 ) : q = (- 48 : 3) : 2

= – 16 : 2

= – 8

- Bilangan Pecahan

Pengertian

Pecahan dapat kita artikan sebagai bagian dari keseluruhan. Dalam ilmu matematika, pacahan adalah bentuk bilangan yang disajikan dalam bentuk a/b, dengan a, b merupakan bilangan bulat dan a bukan kelipatan dari b, serta b ≠ 0. Dalam pecahan juga kita mengenal pembilang dan penyebut, a/b, dimana a sebagai pembilang dan b sebagai penyebut.

Jenis-jenis pecahan
- Pecahan biasa, contohnya 1/2, -12/24, 5/7
- pecahan campuran, contohnya 2 4/9, 2 1/2
- pecahan desimal, contohnya 0,02; 2,50
- persen, contohnya 5%, 25%, 2 4/5%
- permil, contohnya 5‰, 14‰, 25‰

Pecahan senilai merupakan bentuk pecahan yang nilainya sama, walaupun pembilang dan penyebutnya berbeda. Pecahan senilai dapat kita peroleh dengan mengalikan atau membagi pembilang dan penyebutnya dengan bilangan yang sama.

Cara menyederhanakan pecahan
Suatu bentu pecahan dapat kita sederhanakan dengan cara membagi pembilang dan penyebutnya dengan faktor persekutuan terbesar (FPB) dari pembilang dan penyebut pecahan tersebut.

Cara membandingkan dua pecahan
Untuk menegatahui hubungan antara dua pecahan, yang sahabat lakukan adalah dengan terlebih daulu menyamakan penyebutnya dengan cara mencari kelipatan perseketuan terkecil (KPK) dari kedua penyebut pecahan tersebut.

Pecahan campuran
Pecahan campuran merupakan bentuk pecahan yang dapat diubah menjadi bilangan yang terdiri dari bilanagn bulat dan bilangan pecahan itu sendiri. Pecahn campuran juga dapat diubah menjadi pecahan biasa, caranya:
a b/c = (a x c) + b/c

Untuk lebih jelasnya, sahabat bisa mempelajari contoh-contoh di bawah ini:
Menenuntukan pecahan senilai.
3/4 = 3 x 2/4 x 2 = 6/8 atau 3 x 5/4 x 5 = 15/20, jadi 3/4 = 6/8 = 15/20
32/40 = 32 : 2/40 : 2 = 16/20 atau 32 : 4/40 : 4 = 8/10, jadi 32/40 = 16/20 = 8/10

1. Pembulatan Pecahan

Perhatikan aturan pembulatan pecahan desimal berikut ini.

a. Apabila angka yang akan dibulatkan lebih besar atau sama

dengan 5, maka dibulatkan ke atas (angka di depannya atau di

sebelah kirinya ditambah dengan 1).

b. Apabila angka yang akan dibulatkan kurang dari 5, maka angka

tersebut dihilangkan dan angka di depannya (di sebelah kirinya)

tetap.

Contoh

Bulatkan pecahan desimal berikut sampai dua tempat desimal.

a. 0,7921

b. 6,326

c. 1,739

Penyelesaian

a. 0,7921 = 0,79 (angka 2 < 5 dihilangkan)

b. 6,326 = 6,33 (angka 6 > 5, maka angka 2 dibulatkan ke atas)

c. 1,739 = 1,74 (angka 9 > 5, maka angka 3 dibulatkan ke atas)

Untuk menghindari kesalahan dalam pembulatan, jangan

membulatkan bilangan dari hasil pembulatan sebelumnya.

Perhatikan contoh berikut.

3,63471 = 3,635 (benar, pembulatan sampai 3 tempat desimal)

= 3,64 (salah, seharusnya pembulatan dilakukan dari bilangan semula)

3,63471 = 3,63 (pembulatan sampai 2 tempat desimal)

2. Menaksir Hasil Operasi Hitung Pecahan

Kita telah mempelajari cara menaksir hasil perkalian dan

pembagian pada bilangan bulat. Hal tersebut juga berlaku untuk

menaksir hasil perkalian dan pembagian pada bilangan desimal.

Perhatikan contoh berikut.

Taksirlah hasil operasi pada bilangan pecahan berikut.

a. 3,23 x 2,61

b. 15,20 x 3,14

c. 83,76 : 12,33

d. 311,95 : 26,41

Penyelesaian

a. 3,23 x 2,61 ≈ 3 x 3 = 9

b. 15,20 x 3,14 ≈ 15 x 3 = 45

c. 83,76 : 12,33 ≈ 84 : 12 = 7

d. 311,95 : 26,41 ≈ 312 : 26 = 12

3. Bentuk Baku Pecahan

Dalam bidang ilmu pengetahuan alam, sering kali kalian

menemukan bilangan-bilangan yang bernilai sangat besar maupun

sangat kecil. Hal ini terkadang membuat kalian mengalami

kesulitan dalam membaca ataupun menulisnya.

Misalnya sebagai berikut.

a. Panjang jari-jari neutron kira-kira 0,000 000 000 000 00137 m.

b. Jumlah molekul dalam 18 gram air adalah 602.000.000.000.000.000.000.000.

Untuk mengatasi kesulitan tersebut, ada cara yang lebih singkat dan

lebih mudah, yaitu dengan menggunakan notasi ilmiah yang sering

disebut penulisan bentuk baku. Dalam penulisan bentuk baku,

digunakan aturan-aturan seperti pada perpangkatan bilangan.

Perhatikan perpangkatan pada bilangan pokok 10 berikut ini.

10¹ = 10

10² = 10 x 10 = 100

$10^{4}$ = 10 x 10 x 10 x 10 = 10.000

$10^{6}$ = 10 x 10 x 10 x 10 x 10 x 10 = 1.000.000

$10^{0}$ = 1

$10^{-1}=\frac{1}{10^{1}}=\frac{1}{10}$

$10^{-2}=\frac{1}{10^{2}}=\frac{1}{100}$

$10^{-3}=\frac{1}{10^{3}}=\frac{1}{1000}$

dan seterusnya.

Jika dituliskan dalam bentuk baku maka diperoleh

a. panjang jari-jari neutron = 0,000 000 000 000 00137 m = 1,37 x 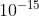$10^{-15}$ m;

b. jumlah molekul dalam 18 gram air =

602.000.000.000.000.000.000.000 = 6,02 x 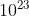$10^{23}$ .

Secara umum, ada dua aturan penulisan bentuk baku suatu

bilangan, yaitu bilangan antara 0 sampai dengan 1 dan bilangan

yang lebih dari 10 sebagai berikut.

Bentuk baku bilangan lebih dari 10 dinyatakan dengan a x 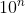$10^{n}$

dengan 1 ≤ a < 10 dan nbilangan asli. Bentuk baku bilangan antara

0 sampai dengan 1 dinyatakan dengan a x $10^{-n}$ dengan 1 ≤ a <

10 dan n bilangan asli.

Contoh

1. Nyatakan bilangan-bilangan berikut dalam bentuk baku.

a. 635.000

b. 258.637.000

Penyelesaian:

a. 635.000 = 6,35 x 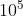$10^{5}$

b. 258.637.000 = 2,58637 x 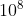$10^{8}$ = 2,59 x 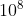$10^{8}$ (pembulatan sampai 2 tempat desimal)

Matematika Kelas 7

Selasa, 05 Februari 2019

Bilangan Bulat dan Bilangan Pecahan

Tidak ada komentar:

Posting Komentar

Segitiga dan Segi Empat

Laporkan Penyalahgunaan